Dans cet article qui fait suite de la partie III, nous allons (re)voir quelques outils classiques d’analyse exploratoire disponibles dans le package Pandas, que l’on met en général en oeuvre pour avoir une meilleure connaissance du jeu de données à étudier avant de passer à l’étape de modélisation à proprement parler.
Nous apprendrons également à manipuler certains outils de pré-traitement des données disponibles dans le module PreProcessing de scikit-learn, permettant d’appliquer diverses transformations aux descripteurs : standardisation, imputation de données manquantes, …
Ressource consulté: hands on machine learning with scikit-learn and tensorflow. Nous travaillerons à partir du jeu de données California Housing, et plus précisemment d’une version sensiblement modifiée, préparée par l’auteur du livre consulté.
1. Chargement du jeu de données housing.csv en utilisant la fonction read_csv du package pandas
In [2]:
# standard imports
import numpy as np
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
# load dataset
housing = pd.read_csv("housing.csv")
2. Aanalyse des propriétés générales du jeu de données via les méthodes info et describe de la classe DataFrame.
In [3]:
# show general properties housing.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 20640 entries, 0 to 20639 Data columns (total 10 columns): longitude 20640 non-null float64 latitude 20640 non-null float64 housing_median_age 20640 non-null float64 total_rooms 20640 non-null float64 total_bedrooms 20433 non-null float64 population 20640 non-null float64 households 20640 non-null float64 median_income 20640 non-null float64 median_house_value 20640 non-null float64 ocean_proximity 20640 non-null object dtypes: float64(9), object(1) memory usage: 1.6+ MB
In [4]:
# show feature summary housing.describe()
Out[4]:
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | |
|---|---|---|---|---|---|---|---|---|---|
| count | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20433.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 |
| mean | -119.569704 | 35.631861 | 28.639486 | 2635.763081 | 537.870553 | 1425.476744 | 499.539680 | 3.870671 | 206855.816909 |
| std | 2.003532 | 2.135952 | 12.585558 | 2181.615252 | 421.385070 | 1132.462122 | 382.329753 | 1.899822 | 115395.615874 |
| min | -124.350000 | 32.540000 | 1.000000 | 2.000000 | 1.000000 | 3.000000 | 1.000000 | 0.499900 | 14999.000000 |
| 25% | -121.800000 | 33.930000 | 18.000000 | 1447.750000 | 296.000000 | 787.000000 | 280.000000 | 2.563400 | 119600.000000 |
| 50% | -118.490000 | 34.260000 | 29.000000 | 2127.000000 | 435.000000 | 1166.000000 | 409.000000 | 3.534800 | 179700.000000 |
| 75% | -118.010000 | 37.710000 | 37.000000 | 3148.000000 | 647.000000 | 1725.000000 | 605.000000 | 4.743250 | 264725.000000 |
| max | -114.310000 | 41.950000 | 52.000000 | 39320.000000 | 6445.000000 | 35682.000000 | 6082.000000 | 15.000100 | 500001.000000 |
In [5]:
# show first lines housing.head()
Out[5]:
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | NEAR BAY |
| 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | NEAR BAY |
| 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | NEAR BAY |
| 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | NEAR BAY |
| 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | NEAR BAY |
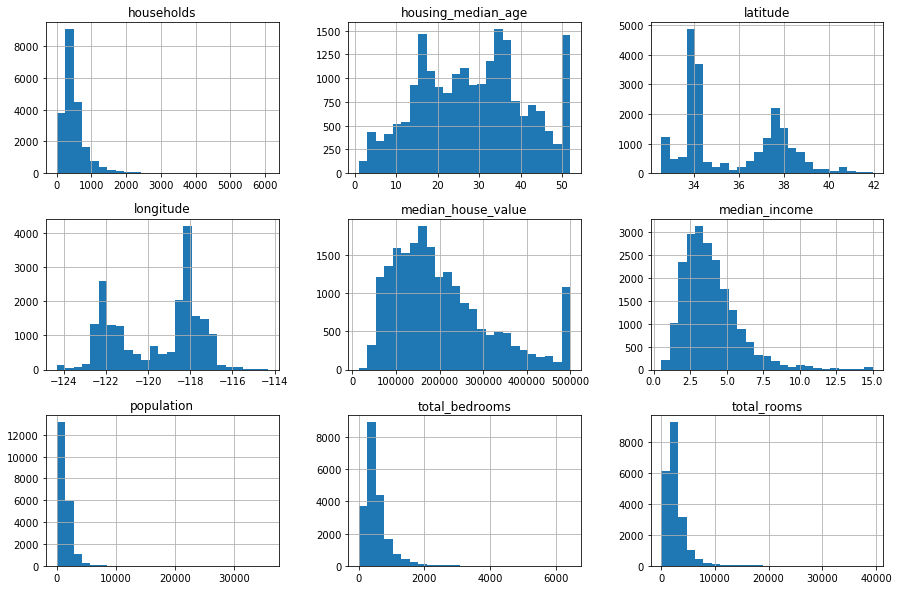
3. Représentation des distributions des descripteurs quantitatifs en utilisant la méthode hist de la classe DataFrame.
- NB : il n’est pas nécessaire de sélectionner au préalable les descripteurs quantitatifs, la fonction hist les sélectionne automatiquement.
In [6]:
housing.hist(bins = 25, figsize=(15,10)) plt.show()
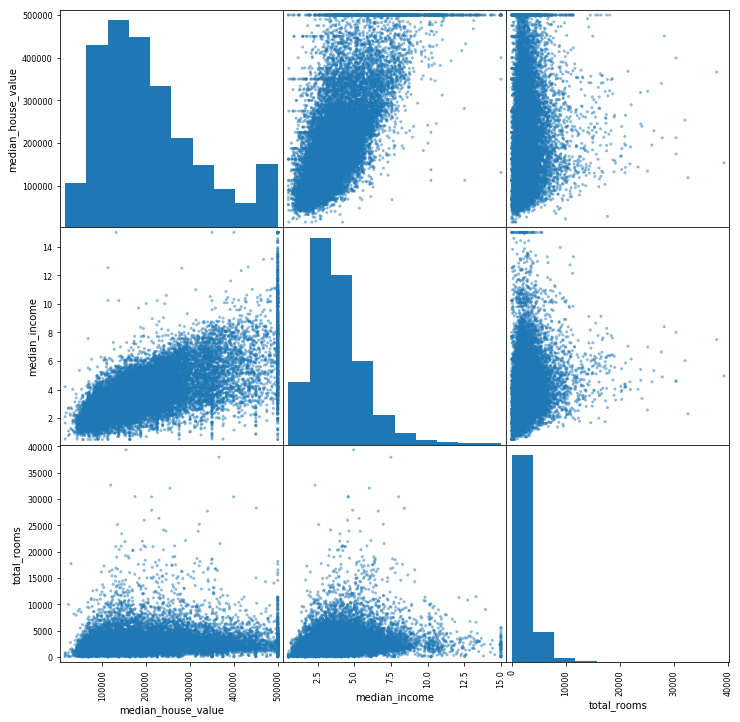
4. Représentation des corrélations entre les descripteurs median_house_value, median_income et total_rooms via la fonction scatter_matrix (à importer du module pandas.plotting).
In [7]:
from pandas.plotting import scatter_matrix vars_plot = ['median_house_value','median_income','total_rooms'] scatter_matrix(housing[vars_plot], figsize = (12,12)) plt.show(scatter_matrix)
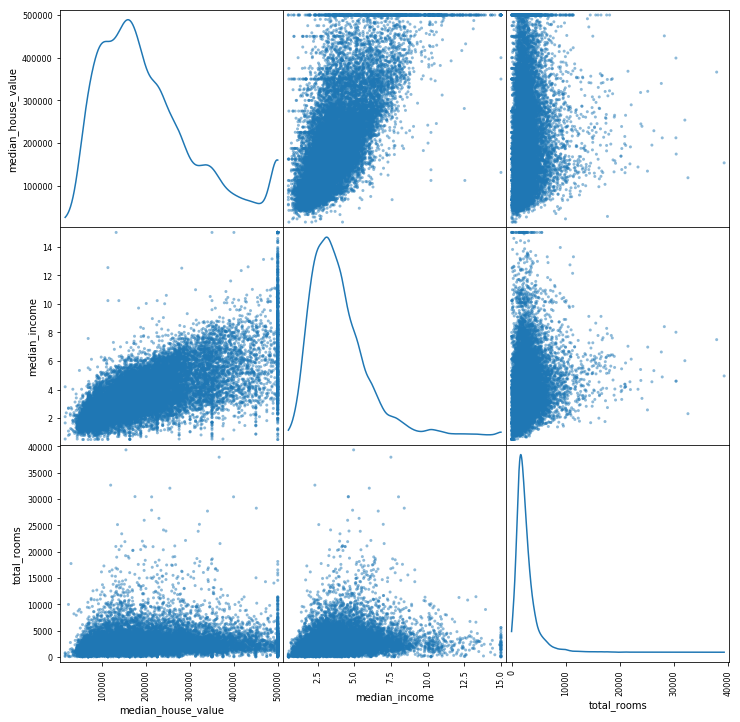
In [8]:
scatter_matrix(housing[vars_plot], figsize = (12,12), diagonal = 'kde') plt.show(scatter_matrix)
5. Nous allons à présent mettre en forme le jeu de données :
1) Extraction de la variable d’intérêt (à prédire) qui est la variable median_house_value .
- Nous allons séparer le jeu de données en variables explicatives (features) et variable à expliquer (réponse).
- On pourra notamment utiliser la méthode drop des DataFrames de Pandas
In [9]:
outcome = housing['median_house_value']
features = housing.drop('median_house_value', axis = 1)
2) Mettons en forme les descripteurs quantitatifs grace au code ci-dessous.
Ceci permet d’extraire les descripteurs, imputer les données manquantes par la méthode de la médiane et les standardiser. Ensuite, vérifier que les valeurs stockées dans le champ statistics_ de l’objet Imputer correspondent bien aux valeurs médianes des descripteurs. In [10]:
# discard qualitative features : median-based imputation only valid for quantitative variables
features_num = features.drop("ocean_proximity", axis = 1)
# import Imputer class and instantiate
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy = "median")
# fit imputer
imputer.fit(features_num)
# apply imputer
X_input = imputer.transform(features_num)
# apply standardization
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# fit scaler
scaler.fit(X_input)
# apply scaler
X_std = scaler.transform(X_input)
In [11]:
features_num.median()
Out[11]:
longitude -118.4900 latitude 34.2600 housing_median_age 29.0000 total_rooms 2127.0000 total_bedrooms 435.0000 population 1166.0000 households 409.0000 median_income 3.5348 dtype: float64
In [12]:
imputer.statistics_
Out[12]:
array([ -118.49 , 34.26 , 29. , 2127. , 435. ,
1166. , 409. , 3.5348])
In [13]:
scaler.mean_
Out[13]:
array([ -119.56970446, 35.63186143, 28.63948643, 2635.7630814 ,
536.83885659, 1425.47674419, 499.53968023, 3.870671 ])
In [14]:
scaler.var_
Out[14]:
array([ 4.01394488e+00, 4.56207160e+00, 1.58388586e+02,
4.75921451e+06, 1.75881025e+05, 1.28240832e+06,
1.46168958e+05, 3.60914769e+00])
3) Le descrpiteur ocean_proximity étant qualitatif. Nous allons l’extraire, et le convertir en variable quantitative par la méthode “one-hot encoding” avec le code ci-dessous.
- notons au passage que la fonction value_counts du package Pandas est l’équivalent de la fonction table de R: elle permet de compter les effectifs des différentes modalités d’une variable qualitative.
In [15]:
housing_cat = housing['ocean_proximity'] # import encoder and instantiate from sklearn.preprocessing import LabelBinarizer encoder = LabelBinarizer() # fit & transform Xcat = encoder.fit_transform(housing_cat)
In [16]:
Xcat.shape
Out[16]:
(20640, 5)
In [17]:
housing_cat.value_counts()
Out[17]:
<1H OCEAN 9136 INLAND 6551 NEAR OCEAN 2658 NEAR BAY 2290 ISLAND 5 Name: ocean_proximity, dtype: int64
4) Fusionnons les descripteurs quantitatifs et qualitatifs mis en forme avec la fonction concatenate du package NumPy
In [18]:
# merge data Xfull = np.concatenate([X_std, Xcat], axis = 1)
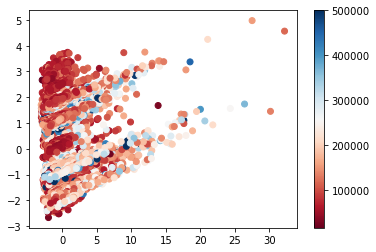
6. Réalisons une analyse en composante principale du jeu de données.
- on considèrera 2 composantes pour l’ACP.
- on utilisera la variable à expliquer comme code couleur pour la représentation
In [19]:
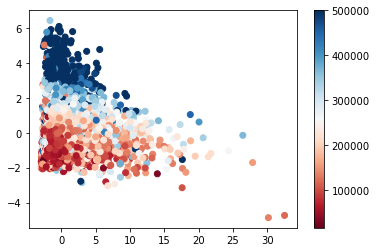
# fit PCA (with 2 PCs) from sklearn.decomposition import PCA pca = PCA(n_components = 2) pca.fit(Xfull) # get coordinates in PC space Xfull_pca = pca.transform(Xfull) # plot plt.scatter(Xfull_pca[:,0], Xfull_pca[:,1], c = outcome, cmap = plt.cm.RdBu) plt.colorbar() plt.show()
7. Comparons à ce que l’on obtient après avoir supprimé les variables longitude et latitude, qui structurent fortement le jeu de données.
In [22]:
# same but discard longitude & latitude X_std_bis = X_std[:,2:] Xfull_bis = np.concatenate([X_std_bis, Xcat], axis = 1) # fit PCA (with 2 PCs) pca.fit(Xfull_bis) # get coordinates in PC space Xfull_bis_pca = pca.transform(Xfull_bis) # plot plt.scatter(Xfull_bis_pca[:,0], Xfull_bis_pca[:,1], c = outcome,cmap = plt.cm.RdBu) plt.colorbar() plt.show()