En machine Learning, l’une des étapes essentielle pour une bonne prédiction est l’étape du feature engineering. Lors de cette étapes plusieurs méthodes sont utilisées pour trouver les meilleurs features parmi l’ensemble de features contenues dans notre data base pour son modèle. En effet, parmi ces techniques, figure l’indice de corrélation couramment utilisée pour trouver une relation entre deux variables quantitatives. Aussi le test de khi2 pour ce qui est des variables qualitatives.

Quel type de relation l’indice de corrélation permet réellement de mesure ?

Comme vous pouvez imaginer l’indice de corrélation ne sert qu’à détecter d’éventuelle relation linéaire entre deux variables quantitatives. Autrement dire, qu’on peut approximer la variable dépendante à l’aide d’un ajustement linéaire des variables indépendantes. Toutefois dans la vie pratique, il n’est pas évident que tout le variable incluant notre base de données soit toute linéairement corrélé avec notre variable à prédire. Dans la suite, nous ferons un exemple afin de mieux illustrer ce problème.

Description data

Nous allons illustrer la relation avec une simulation de données uniforme. En effet, notre features sera une variable suivant une loi uniforme tandis que les targets seront lié avec cette dernière par soit une relation quadratique, sinusoïdale ou encore polynomiale.

In [100]: import pandas as pd,numpy as np
data=pd.DataFrame([np.random.uniform(-5,5)	for i in range(5000)],columns=['features data['targets_quadratique']= data.features**2
data['targets_sinus']= np.sin(data.features)
data['targets_ploly']= data.features**3 + data.features**2 + data.features

Indice de correlation

In [101]: import matplotlib.pyplot as plt
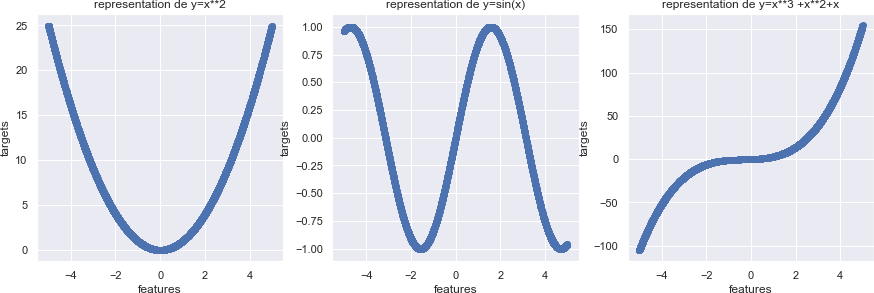
fig,ax=plt.subplots(figsize=(15,10)) plt.subplot(231) plt.scatter(data.features,data.targets_quadratique) plt.xlabel("features")
plt.ylabel("targets") plt.title("representation de y=x**2") plt.subplot(232) plt.scatter(data.features,data.targets_sinus)
 
plt.xlabel("features") plt.ylabel("targets") plt.title("representation de y=sin(x)") plt.subplot(233)
plt.scatter(data.features,data.targets_ploly) plt.xlabel("features")
plt.ylabel("targets") plt.title("representation de y=x**3 +x**2+x")
Out[101]: Text(0.5, 1.0, 'representation de y=x**3 +x**2+x')

In [102]:
Out[102]:	data.corr()	
features	
targets_quadratique	
targets_sinus	\
	features	1.000000	0.002368	-0.228784
	targets_quadratique	0.002368	1.000000	0.000069
	targets_sinus	-0.228784	0.000069	1.000000
	targets_ploly	0.915778	0.143604	-0.522612

features	targets_ploly
0.915778
targets_quadratique	0.143604
targets_sinus	-0.522612
targets_ploly	1.000000
In [104]: import matplotlib.pyplot as plt
sns.set() sns.pairplot(data) plt.savefig('corr.png')

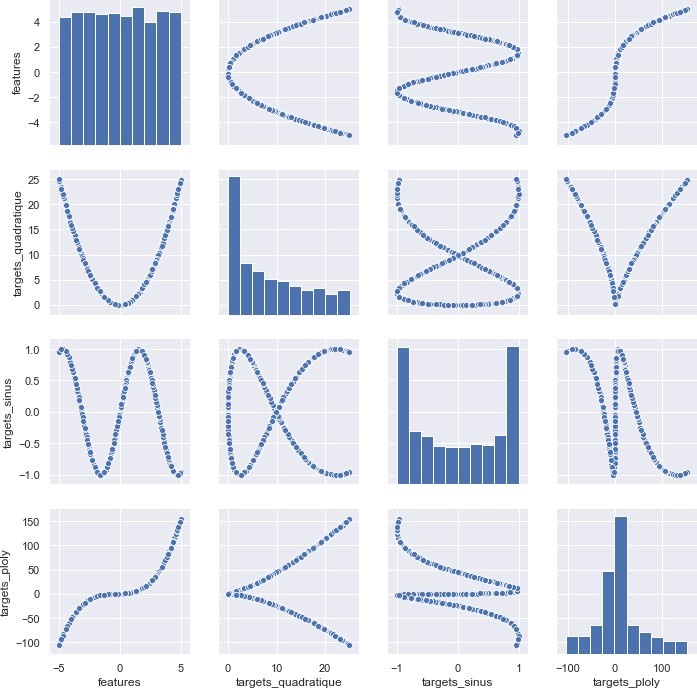
Vous pouvez constater que seule la relation polynomiale est détectée. Pourtant, toutes les variables ont été créé avec le même feature et des relations bien connues de tous. Ceci montre en effet, l’importance de bien comprendre les données. Une alternative à cela est l’utilisation d’autres méthodes servant à trouver des relations non-linéaire entre deux variables. Un Plusieurs méthodes existes notamment, Récursive feature élimination(RFE) , Random forest, Predictive power scores (ppscore) etc… Dans cet article, nous allons prendre comme exemple ppscores

ppscore PPS ou encore prédictive power score est une technique utilisant l’arbre de décision avez une validation croisée pour pouvoir capter d’éventuelle lien entre deux variables qu’elle soit qualitative ou quantitative.

In [106]: #!pip install ppscore
import ppscore as pps import warnings
warnings.filterwarnings("ignore")
 
val_index=pps.matrix(data) val_index

Out[106]:		features	targets_quadratique	targets_sinus	\
	features	1.000000	0.000000	0	
	targets_quadratique	0.998947	1.000000	0	
targets_sinus	0.998659	0.011921	1
targets_ploly	0.998991	0.000000	0

features	targets_ploly
0.999459		
targets_quadratique	0.998947		
targets_sinus	0.998659		
targets_ploly	1.000000		
In [107]: sns.heatmap(val_index,annot=True,fmt='.2f') plt.savefig('pps.png')

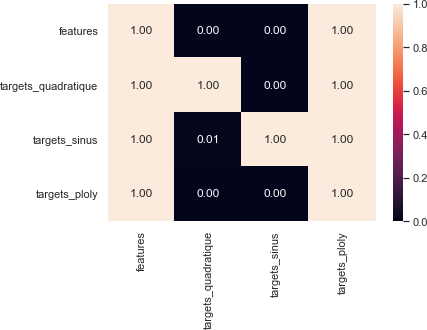
Vous pouvez constater que vous arrivez à déceler certaines relations non linéaires qui étaient invisible avec la corrélation. Toutefois, il existe d’autres relation assez difficile à modélisation dont vous aurez à faire recourt à plusieurs algorithmes afin de les détecter. Vous pouvez toutefois, aller en crécha do tout en commençant votre étude par la détection de relation linéaire. Aussi, le type de relation peut vous aider au choix d’algorithme de machine Learning à utiliser.